Filtr pasmowy jest jednym z kluczowych narzędzi współczesnej techniki, umożliwiającym selekcję wybranych fragmentów widma sygnału przy jednoczesnym tłumieniu pozostałych częstotliwości. Pozwala to na niezawodne przesyłanie informacji, redukcję szumów i optymalizację działania niezliczonych urządzeń, od radioodbiorników, przez systemy medyczne, aż po zaawansowane eksperymenty fizyczne. Zrozumienie działania filtru pasmowego wymaga połączenia wiedzy z zakresu elektrotechniki, matematyki, teorii sygnałów i fizyki fal.
Podstawy teoretyczne działania filtru pasmowego
Filtr pasmowy to układ, który przepuszcza sygnały z ograniczonego zakresu częstotliwości – tzw. pasma przepustowego – jednocześnie tłumiąc sygnały o częstotliwościach niższych i wyższych. Można go traktować jako połączenie filtru dolnoprzepustowego oraz górnoprzepustowego, działających w taki sposób, aby z całego widma sygnału wyodrębnić interesującą nas część.
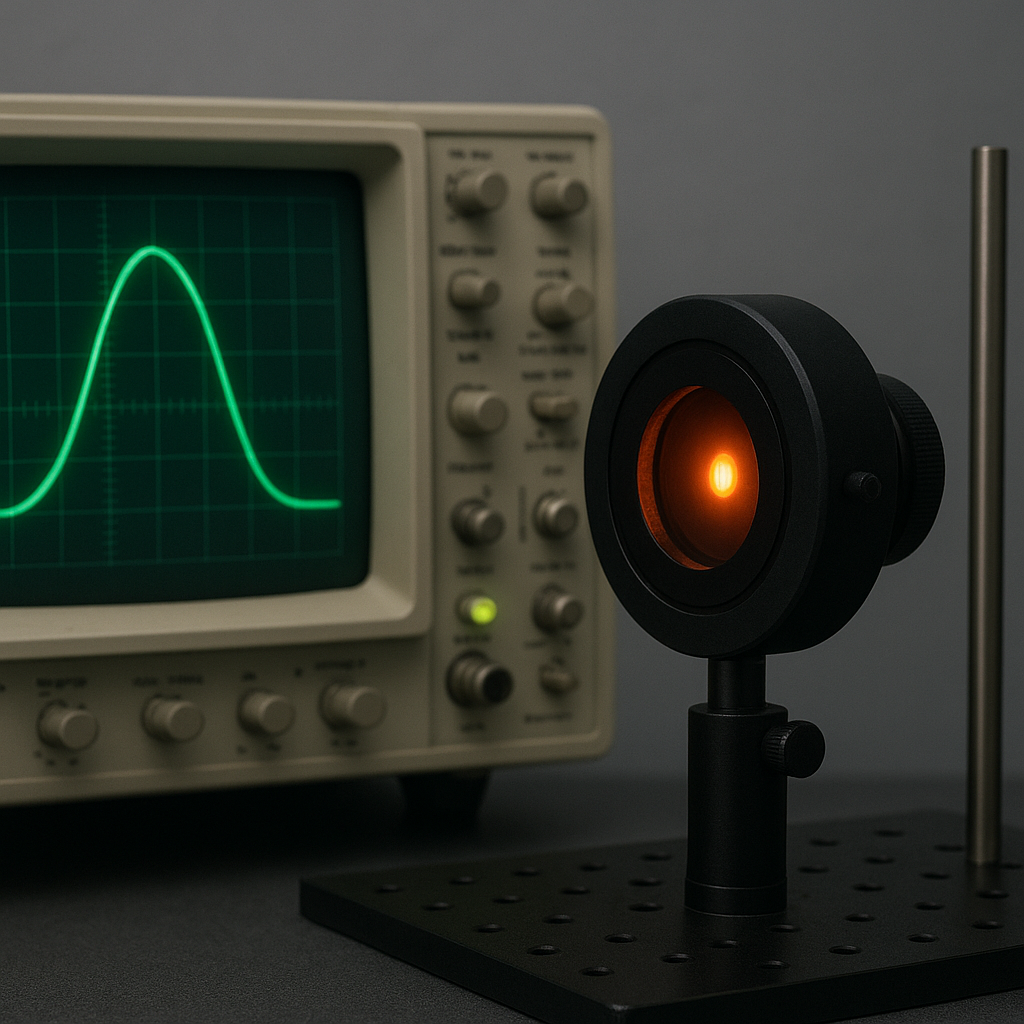
Matematycznie działanie filtru pasmowego opisuje się za pomocą jego charakterystyki częstotliwościowej, czyli funkcji przenoszenia H(f), określającej stosunek amplitudy (oraz przesunięcia fazowego) sygnału wyjściowego do wejściowego w funkcji częstotliwości. W idealnym przypadku filtr pasmowy miałby charakterystykę prostokątną: w paśmie przepustowym transmitancja byłaby stała, a poza nim – równa zeru. W praktyce filtry są nieidealne, posiadają skończone zbocza i ograniczone tłumienie poza pasmem.
Podstawowe parametry opisujące filtr pasmowy to:
- częstotliwość dolna fL – granica dolna pasma przepustowego, poniżej której sygnał jest znacząco tłumiony,
- częstotliwość górna fH – granica górna pasma przepustowego, powyżej której sygnał jest tłumiony,
- częstotliwość środkowa f0 – najczęściej definiowana jako geometryczna średnia f0=√(fL·fH),
- szerokość pasma B = fH − fL,
- współczynnik jakości Q = f0/B, opisujący „wąskość” pasma.
Wysoka wartość współczynnika jakości oznacza, że filtr pasmowy ma bardzo wąskie pasmo przepustowe i jest zdolny do precyzyjnego wybierania częstotliwości. Takie filtry stosuje się m.in. w odbiornikach radiowych i systemach radarowych. Niska wartość Q oznacza filtr szerokopasmowy, wykorzystywany np. do ogólnej redukcji szumu lub kształtowania widma w systemach audio.
Filtr pasmowy można rozpatrywać również w dziedzinie czasu. Impulsowa odpowiedź takiego filtru jest zwykle zbliżona do tłumionej sinusoidy, której częstotliwość odpowiada częstotliwości środkowej. Z punktu widzenia teorii sygnałów oznacza to, że filtr pasmowy silnie reaguje na sygnały zbliżone do swojej częstotliwości rezonansowej, a słabo – na pozostałe składowe widma.
Z fizycznego punktu widzenia mechanizm działania filtru pasmowego często wiąże się z rezonansowym zachowaniem układu. Przykładowo obwód RLC (rezystor, cewka, kondensator) może przy odpowiedniej konfiguracji „wzmacniać” sygnały w okolicy częstotliwości rezonansowej, a tłumić inne. Rezonans jest uniwersalnym zjawiskiem, spotykanym nie tylko w elektronice, ale także w akustyce, optyce, mechanice i fizyce kwantowej, co czyni filtr pasmowy pojęciem przekraczającym granice pojedynczych dyscyplin.
Rodzaje filtrów pasmowych i ich realizacje
Filtry pasmowe można podzielić na wiele sposobów: według fizycznej realizacji (analogowe, cyfrowe), typu elementów (RLC, aktywne, oparte na falowodach, optyczne), funkcji matematycznej (Butterwortha, Czebyszewa, Bessela, eliptyczne) czy sposobu implementacji (układy scalone, algorytmy komputerowe, struktury mikrofalowe). Każde z tych rozwiązań ma własne zalety, ograniczenia oraz typowe obszary zastosowań.
Filtry pasmowe analogowe
W klasycznym ujęciu filtr pasmowy analogowy to układ zbudowany z elementów pasywnych R, L, C lub kombinacji tych elementów z wzmacniaczami operacyjnymi. Podstawowe topologie to:
- obwody RLC w konfiguracji szeregowej lub równoległej,
- aktywny filtr pasmowy z wykorzystaniem wzmacniacza operacyjnego i sprzężenia zwrotnego,
- filtry oparte na multiplekserach, przełączanych kondensatorach czy układach Gm-C.
Szeregowy obwód RLC przy zasilaniu napięciem sinusoidalnym charakteryzuje się minimalną impedancją dla częstotliwości rezonansowej f0. W okolicy tej częstotliwości prąd w obwodzie przyjmuje największą wartość, co pozwala na wykorzystanie tego zjawiska do selekcji pasma. Równoległy obwód RLC zachowuje się odwrotnie – jego impedancja przy rezonansie jest maksymalna, co także można wykorzystać w konstrukcji filtru pasmowego, szczególnie w układach wejściowych odbiorników radiowych.
Filtry aktywne, wykorzystujące wzmacniacze operacyjne, pozwalają realizować precyzyjne charakterystyki przy użyciu wyłącznie elementów R i C, eliminując konieczność stosowania cewek. To szczególnie ważne w urządzeniach małogabarytowych, gdzie stosowanie indukcyjności jest utrudnione lub kosztowne. Dzięki sprzężeniu zwrotnemu możliwe jest również uzyskiwanie wysokiej dynamiki oraz łatwa regulacja częstotliwości środkowej i szerokości pasma.
W praktycznych konstrukcjach istotne są również tzw. klasy aproksymacji charakterystyki amplitudowej. Najczęściej stosowane rodziny filtrów to:
- Butterwortha – o maksymalnie płaskim paśmie przepustowym,
- Czebyszewa – o mniejszych zboczach i większym nachyleniu tłumienia kosztem pofalowania w paśmie,
- Bessela – zapewniające minimalne zniekształcenia fazowe kosztem mniej stromej charakterystyki amplitudowej,
- eliptyczne – o najbardziej stromej charakterystyce przy dopuszczeniu pofalowań w paśmie przepustowym i zaporowym.
Filtry pasmowe cyfrowe
Cyfrowy filtr pasmowy jest realizowany w postaci algorytmu, który przetwarza próbkowany sygnał. Zamiast elementów RLC stosuje się operacje arytmetyczne na próbkach sygnału, takie jak sumowanie, mnożenie, przesunięcia w czasie oraz różnicowanie. Sercem takiego filtru jest jego odpowiedź impulsowa, czyli zbiór współczynników, przez które mnoży się kolejne próbki.
Cyfrowe filtry pasmowe dzielimy głównie na:
- FIR (Finite Impulse Response) – o skończonej odpowiedzi impulsowej, zawsze stabilne, łatwe do zaprojektowania z liniową fazą,
- IIR (Infinite Impulse Response) – o nieskończonej odpowiedzi impulsowej, zbliżone do analogowych filtrów RLC, bardziej efektywne obliczeniowo, ale trudniejsze w zapewnieniu stabilności.
Cyfrowa realizacja filtru pasmowego pozwala osiągnąć niezwykle precyzyjne charakterystyki, a także dynamiczną zmianę parametrów w czasie pracy systemu. Jest to kluczowe w nowoczesnych systemach komunikacyjnych, takich jak LTE, Wi-Fi czy 5G, gdzie algorytmy filtracji są implementowane w dedykowanych procesorach sygnałowych (DSP) lub w programowalnych układach FPGA.
W praktyce projekt filtru cyfrowego opiera się na narzędziach matematycznych, takich jak transformata Z, metoda okien, iteracyjna optymalizacja (np. algorytmy Parks–McClellan) czy okołonajlepsze aproksymacje w sensie normy minimaksowej. Wykorzystanie transformaty Fouriera umożliwia łatwe przechodzenie między opisem w dziedzinie czasu i częstotliwości oraz intuicyjną wizualizację efektu filtracji.
Filtry pasmowe w wysokich częstotliwościach i mikrofali
W obszarze częstotliwości mikrofalowych oraz fal milimetrowych filtrów pasmowych nie buduje się w klasyczny sposób z elementów skupionych RLC, lecz z wykorzystaniem struktur rozłożonych: linii mikropaskowych, falowodów, rezonatorów dielektrycznych czy wnęk rezonansowych. W tym zakresie fale elektromagnetyczne mają wymiary porównywalne z rozmiarem elementów obwodu, przez co konieczne jest stosowanie teorii linii długich oraz równań Maxwella.
Takie filtry pasmowe odgrywają decydującą rolę w systemach satelitarnych, radarach, radiolokacji, łączności wojskowej i urządzeniach 5G. Dążenie do miniaturyzacji i zwiększania częstotliwości pracy prowadzi do intensywnego rozwoju nowoczesnych technologii, takich jak filtry oparte na rezonatorach nadprzewodzących, strukturach fotonicznych czy metamateriałach o zaprojektowanej permittiwności i przenikalności magnetycznej.
Filtry pasmowe w optyce
W optyce pojęcie filtru pasmowego dotyczy selekcji wąskiego zakresu długości fali światła. Typowym przykładem są filtry interferencyjne, które dzięki zjawisku wielokrotnego odbicia w cienkich warstwach dielektrycznych przepuszczają tylko wybrane barwy. Odpowiednikiem częstotliwości jest tutaj odwrotność długości fali, a charakterystyka pasmowa opisuje, jakie zakresy widma elektromagnetycznego są transmitowane.
Optyczne filtry pasmowe są niezbędne w spektroskopii, laserach, telekomunikacji światłowodowej oraz w aparaturze medycznej. Dzięki nim można wydzielać linie emisyjne konkretnych pierwiastków, kompensować zakłócenia świetlne, a także budować systemy multipleksacji długości fali w światłowodach, co drastycznie zwiększa przepustowość nowoczesnych sieci.
Zastosowania filtrów pasmowych w nauce, technice i medycynie
Uniwersalność filtru pasmowego wynika z tego, że większość zjawisk fizycznych można opisywać w kategoriach fal i częstotliwości. W każdej dziedzinie, w której analizuje się sygnały – elektryczne, akustyczne, optyczne czy biologiczne – pojawia się potrzeba selektywnego „odsiania” niepożądanych składowych i skupienia się na tych istotnych. Poniżej przedstawiono wybrane obszary, w których filtr pasmowy ma znaczenie fundamentalne.
Telekomunikacja i systemy radiowe
W systemach radiokomunikacyjnych filtr pasmowy jest jednym z głównych elementów toru wejściowego odbiornika. Każdemu kanałowi radiowemu przyporządkowane jest określone pasmo częstotliwości. Filtr pasmowy pozwala wydzielić to pasmo z mieszaniny sygnałów docierających do anteny, jednocześnie tłumiąc sąsiednie kanały i zakłócenia. Im wyższa selektywność filtru, tym lepsza odporność systemu na interferencje.
W nadajnikach filtry pasmowe pełnią inną, ale równie ważną rolę – ograniczają emisję poza zadanym pasmem, zmniejszając zakłócenia generowane w innych kanałach. Bez skutecznej filtracji pasmowej współistnienie wielu systemów radiowych byłoby praktycznie niemożliwe. Współczesne standardy, takie jak LTE, 5G czy Wi-Fi, stawiają szczególnie wysokie wymagania w zakresie kształtu widma, co przekłada się na złożone konstrukcje filtrów w torach nadawczo-odbiorczych.
Przetwarzanie sygnałów biometrycznych i medycznych
W medycynie filtry pasmowe są nieocenione przy analizie sygnałów takich jak EEG (elektroencefalografia) czy EKG (elektrokardiografia). Sygnały te zawierają wiele składowych częstotliwościowych, z których tylko niektóre są diagnostycznie istotne. Przykładowo w EEG rozróżnia się pasma fal delta, theta, alfa, beta i gamma, a każde z nich niesie informacje o innym stanie pracy mózgu.
Stosując odpowiednio zaprojektowane filtry pasmowe, można wydzielać konkretne pasma częstotliwości, co ułatwia diagnostykę epilepsji, monitorowanie snu czy badanie reakcji na bodźce. W EKG z kolei filtry pasmowe pomagają w eliminacji linii zasilania (50/60 Hz), szumu mięśniowego i innych zakłóceń, tak aby lekarz mógł analizować czystą aktywność elektryczną serca.
W nowoczesnych systemach medycznych filtracja jest realizowana głównie cyfrowo, co umożliwia adaptacyjne dostosowywanie parametrów do konkretnego pacjenta, warunków pomiaru czy rodzaju analizowanego sygnału. Dzięki temu poprawia się zarówno czułość, jak i swoistość metod diagnostycznych, a także komfort pacjentów, ponieważ możliwe jest stosowanie mniej inwazyjnych technik pomiaru.
Akustyka, audio i muzyka
W akustyce filtr pasmowy pełni funkcję „korektora barwy” dźwięku. W systemach nagłośnieniowych, studiach nagrań, a nawet w domowych odtwarzaczach audio stosuje się różne formy filtracji pasmowej do kształtowania brzmienia. Umożliwia to podkreślanie lub wygaszanie określonych pasm częstotliwości, co ma wpływ na czytelność mowy, głębię basu czy klarowność wysokich tonów.
W instrumentach muzycznych i efektach gitarowych filtry pasmowe są elementem odpowiedzialnym za charakterystyczne brzmienie. Przykładem może być efekt „wah-wah”, w którym dynamicznie przesuwa się częstotliwość środkową filtru pasmowego, co daje charakterystyczną modulację barwy. Z kolei w korektorach parametrycznych użytkownik może precyzyjnie regulować częstotliwość środkową, szerokość pasma i wzmocnienie danego pasma, co pozwala na szczegółową kontrolę nad dźwiękiem.
Badania psychoakustyczne pokazują, że ludzkie ucho analizuje dźwięk w kategoriach pasm częstotliwości – tzw. pasm krytycznych. Stanowi to silny argument, by w projektowaniu urządzeń audio i systemów kompresji danych (np. MP3, AAC) wykorzystywać modele filtrów pasmowych zbliżone do biologicznego przetwarzania sygnału w ślimaku. Dzięki temu możliwe jest odrzucanie tych składowych widma, na które ludzkie ucho jest najmniej czułe, bez zauważalnej utraty jakości percepcyjnej.
Eksperymenty naukowe i aparatura pomiarowa
W fizyce eksperymentalnej, chemii analitycznej czy inżynierii materiałowej filtr pasmowy służy do precyzyjnego wydzielania interesujących sygnałów z tła. Przykładowo w spektroskopii modulowanej wykorzystywane jest zjawisko, że sygnał użyteczny pojawia się w określonym paśmie częstotliwości, podczas gdy szum ma charakter szerokopasmowy. Odpowiednio zaprojektowany filtr pasmowy pozwala wtedy znacząco zwiększyć stosunek sygnału do szumu.
W aparaturze do pomiaru drgań, wibroakustyce czy monitoringu konstrukcji inżynierskich filtry pasmowe pomagają analizować konkretne tryby drgań, związane z uszkodzeniami czy zmęczeniem materiału. Dzięki temu możliwe jest wczesne wykrywanie pęknięć, luzów czy innych defektów w mostach, budynkach, samolotach i maszynach przemysłowych.
W badaniach astronomicznych filtry pasmowe – zarówno elektryczne, jak i optyczne – pozwalają „zobaczyć” zjawiska, które w przeciwnym razie ginęłyby w tle promieniowania kosmicznego. W radioteleskopach selekcja częstotliwości umożliwia analizę linii emisyjnych różnych pierwiastków w przestrzeni kosmicznej, a w teleskopach optycznych filtry wąskopasmowe służą do rejestrowania konkretnych linii widmowych, np. wodoru czy tlenu, co dostarcza informacji o składzie chemicznym i procesach zachodzących w odległych obiektach.
Informatyka, uczenie maszynowe i analiza danych
Choć filtr pasmowy kojarzy się głównie z elektroniką, jego idea przenika również do informatyki i nauki o danych. W sygnałach czasowych, takich jak szeregi finansowe, zapisy ruchu sensorów czy dane z sieci społecznościowych, można identyfikować pewne „częstotliwości” zmian. Filtracja pasmowa pozwala izolować określone skale czasowe, co ułatwia analizę trendów, cykli i anomalii.
Coraz częściej stosuje się filtry pasmowe w połączeniu z metodami uczenia maszynowego. Przed podaniem danych do sieci neuronowych czy klasyfikatorów często przeprowadza się wstępne przetwarzanie – w tym ekstrakcję cech w pasmach częstotliwości, które są najbardziej informatywne dla danego zadania. Takie podejście znajduje zastosowanie np. w rozpoznawaniu mowy, analizie emocji na podstawie sygnałów biometrycznych, identyfikacji użytkowników na podstawie ich sposobu chodzenia (gait recognition) czy wykrywaniu zdarzeń w danych IoT.
Znaczenie edukacyjne i interdyscyplinarne
Filtr pasmowy jest także ważnym narzędziem edukacyjnym. Umożliwia spójne wprowadzenie wielu kluczowych pojęć z różnych dziedzin: różniczkowych równań liniowych w matematyce, teorii obwodów w elektrotechnice, transformacji Fouriera w teorii sygnałów, a także zjawisk falowych w fizyce. Dzięki temu stanowi znakomity przykład ilustrujący, jak różne języki opisu – czasowy, częstotliwościowy, przestrzenny – są ze sobą powiązane.
Na zajęciach laboratoryjnych studenci często budują proste filtry pasmowe z elementów RLC, a następnie projektują ich cyfrowe odpowiedniki w środowiskach programistycznych. Pozwala to zrozumieć, jak ta sama koncepcja może przybierać bardzo różne formy fizyczne i matematyczne, zachowując przy tym identyczną funkcję – selekcję określonego zakresu częstotliwości.
FAQ – najczęściej zadawane pytania o filtr pasmowy
Do czego służy filtr pasmowy w praktyce?
Filtr pasmowy służy do przepuszczania sygnałów z określonego zakresu częstotliwości i tłumienia pozostałych. W praktyce oznacza to np. wybór konkretnego kanału radiowego z wielu, redukcję zakłóceń w pomiarach medycznych, kształtowanie barwy dźwięku w systemach audio czy izolowanie interesującego zjawiska w eksperymentach naukowych. Dzięki niemu można skupić się na istotnych informacjach, odfiltrowując szum i niepożądane składowe widma.
Czym różni się filtr pasmowy analogowy od cyfrowego?
Filtr pasmowy analogowy działa bezpośrednio na ciągłym sygnale elektrycznym, wykorzystując elementy takie jak rezystory, kondensatory, cewki i wzmacniacze operacyjne. Filtr cyfrowy przetwarza sygnał po jego próbkowaniu i zamianie na postać liczbową, korzystając z algorytmów wykonywanych w procesorach lub układach FPGA. Cyfrowe filtry oferują większą elastyczność i precyzję kształtowania charakterystyki, ale wymagają konwersji A/C i odpowiedniej mocy obliczeniowej.
Co oznacza częstotliwość środkowa filtru pasmowego?
Częstotliwość środkowa to częstotliwość znajdująca się w centrum pasma przepustowego, zazwyczaj definiowana jako geometryczna średnia częstotliwości dolnej i górnej. Dla tej wartości filtr zwykle ma największe wzmocnienie lub najmniejsze tłumienie. W praktyce częstotliwość środkowa jest tą, wokół której projektuje się działanie filtru: decyduje np. o tym, który kanał radiowy zostanie wybrany, jakie pasmo dźwięku zostanie podkreślone lub jaka linia widmowa będzie analizowana w optyce.
Dlaczego współczynnik jakości Q jest tak ważny?
Współczynnik jakości Q określa, jak wąskie jest pasmo przepustowe w stosunku do częstotliwości środkowej. Wysokie Q oznacza dużą selektywność: filtr przepuszcza bardzo wąski zakres częstotliwości i silnie tłumi składowe sąsiednie. Jest to istotne wszędzie tam, gdzie trzeba rozdzielić bardzo blisko położone sygnały, np. w odbiornikach radiowych lub precyzyjnych systemach pomiarowych. Niskie Q jest korzystne, gdy potrzebne jest szerokie pasmo i łagodniejsze zbocza charakterystyki.
Czy filtr pasmowy może poprawić jakość dźwięku?
Tak, filtr pasmowy jest jednym z podstawowych narzędzi służących do poprawy jakości dźwięku. Dzięki niemu można redukować szumy i przydźwięki, usuwać niepożądane rezonanse pomieszczenia, a także kształtować barwę instrumentów i głosu. W praktyce stosuje się zestawy filtrów pasmowych w korektorach graficznych i parametrycznych, które pozwalają na selektywne wzmacnianie lub osłabianie określonych pasm częstotliwości, dostosowując brzmienie do akustyki sali, preferencji słuchacza lub wymagań realizatora dźwięku.