Fale są jednym z najbardziej fundamentalnych zjawisk w przyrodzie – od drgań struny gitary, przez fale na powierzchni wody, aż po fale elektromagnetyczne i fale materii w mechanice kwantowej. Aby w pełni zrozumieć ich zachowanie, trzeba rozróżnić dwa pojęcia: prędkość, z jaką przemieszcza się kształt fali, oraz prędkość, z jaką przenoszona jest energia i informacja. Ta druga nazywa się prędkością grupową i jest kluczowa zarówno dla współczesnej telekomunikacji, jak i dla zrozumienia ograniczeń stawianych przez relatywistyczną teorię prędkości światła.
Fale, widmo i pojęcie grupy fal
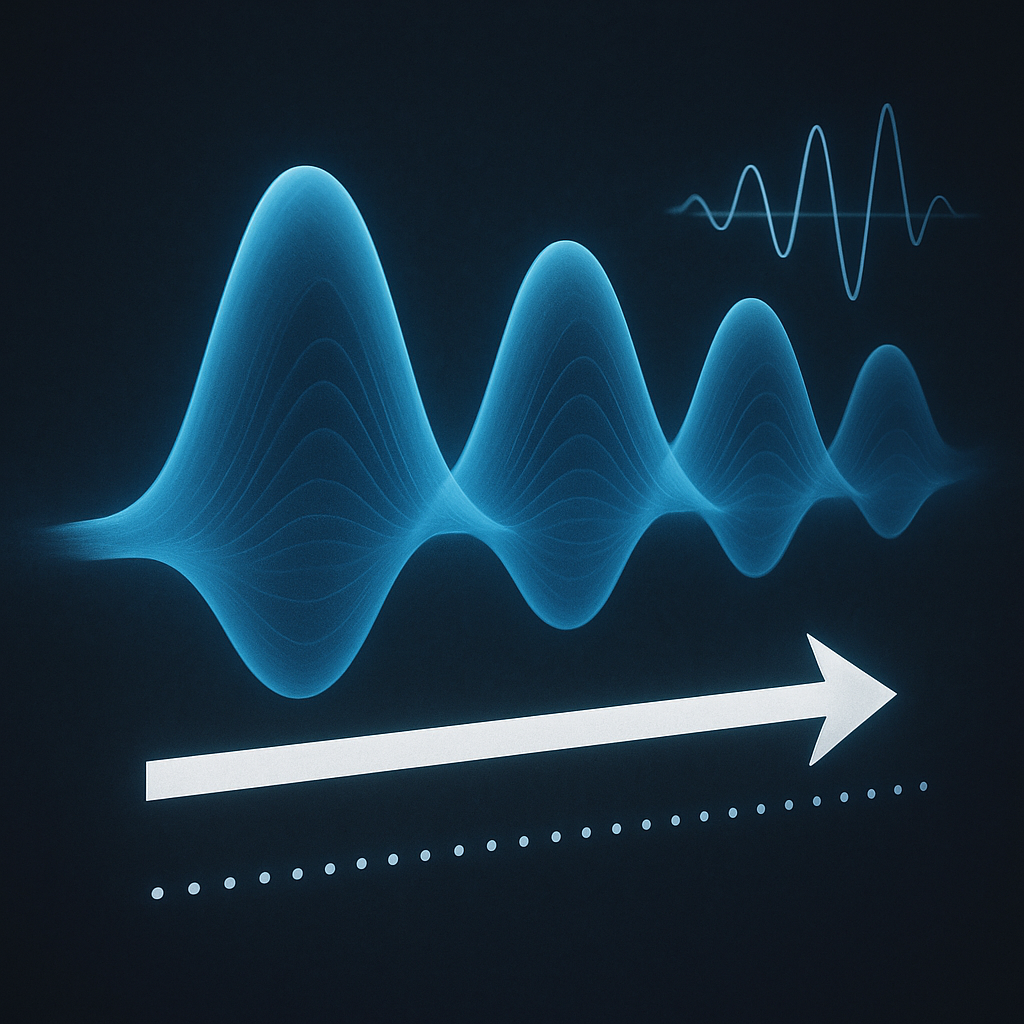
Aby zrozumieć, czym jest prędkość grupowa, warto zacząć od pojęcia pojedynczej fali harmonicznej. Idealna fala sinusoidalna o jednej częstotliwości rozciąga się od minus do plus nieskończoności i nie zmienia swojego kształtu podczas propagacji w ośrodku liniowym i jednorodnym. Taka idealizacja jest jednak fizycznie nierealistyczna: rzeczywiste sygnały – impuls świetlny w światłowodzie, krótki dźwięk czy pakiet fal oceanicznych – są zawsze w jakiś sposób ograniczone w przestrzeni i czasie, mają początek, maksimum i koniec.
Matematycznie opisuje się takie rzeczywiste sygnały jako superpozycję, czyli sumę wielu fal o różnych częstotliwościach i wektorach falowych. Zbiór tych składowych tworzy tak zwane widmo. Jeżeli widmo skupione jest wokół jednej charakterystycznej częstotliwości, mówimy o paczce falowej. W mechanice fal paczka falowa jest wygodnym narzędziem do opisu krótkich impulsów, które niosą energię lub informację z jednego punktu do drugiego. To właśnie ruch maksimum lub obszaru największej amplitudy paczki utożsamia się z prędkością grupową.
Kluczową rolę odgrywa tu zależność między częstością kołową a wektorem falowym, zwana relacją dyspersyjną. Dla danego ośrodka i rodzaju fali relacja ta określa, jakie częstotliwości mogą rozchodzić się z jakimi liczbami falowymi, a tym samym jak układa się widmo paczki falowej. W najprostszym ujęciu prędkość fazowa, opisująca ruch powierzchni stałej fazy, wynika z ilorazu częstości przez liczbę falową, natomiast prędkość grupowa wiąże się z pochodną tej relacji po liczbie falowej. To rozróżnienie jest subtelne, ale ma głębokie konsekwencje dla tego, jak rozchodzi się energia i jak sygnały się zniekształcają.
Rzeczywiste ośrodki rzadko są idealne: zazwyczaj wykazują własności dyspersyjne, co oznacza, że różne częstotliwości rozchodzą się z różnymi prędkościami fazowymi. W takim środowisku paczka falowa z czasem się rozmywa, a jej kształt ulega zmianie. Analiza prędkości grupowej staje się wtedy narzędziem do przewidywania, jak bardzo impuls się wydłuży, jak duże będą zniekształcenia i w jaki sposób można je kompensować.
Matematyczne ujęcie prędkości grupowej
Załóżmy, że mamy do czynienia z falą opisaną ogólnym wyrażeniem zależnym od wektora falowego i częstości. Jeśli zbudujemy paczkę falową jako superpozycję wielu fal o bliskich wartościach liczby falowej, to jej obwiednia – czyli gładka funkcja amplitudy opisująca zasięg i intensywność sygnału – przemieszcza się z prędkością nazywaną grupową. Analiza matematyczna prowadzi do prostego, lecz fundamentalnego wyniku: prędkość grupowa jest pochodną częstości kołowej względem liczby falowej.
Można to zinterpretować następująco: jeśli w widmie paczki dominują składowe o pewnym zakresie liczby falowej, to niewielka zmiana tej liczby falowej powoduje określoną zmianę częstości. Stosunek tych zmian definiuje prędkość, z jaką maksimum obwiedni wędruje po ośrodku. To obwiednia reprezentuje lokalne nagromadzenie energii i pozwala identyfikować region, z którym związane jest przekazywanie informacji. Z punktu widzenia fizyki falowej to właśnie ten region, a nie poszczególne maksima fali harmonicznej, ma bezpośredni sens obserwacyjny.
W przypadku braku dyspersji – gdy prędkość fazowa jest stała i niezależna od liczby falowej – pochodna częstości po liczbie falowej jest równa stałej, co oznacza, że prędkości fazowa i grupowa pokrywają się. W takim idealnym scenariuszu paczka falowa zachowuje swój kształt w nieskończoność, a analiza sygnałów jest szczególnie prosta. Większość interesujących zjawisk w optyce, akustyce czy fizyce materii skondensowanej pojawia się jednak właśnie dlatego, że ta idealna sytuacja jest naruszona.
Rozróżnienie między prędkością fazową a grupową ma znaczenie nie tylko formalne. Przy opisie mechaniki kwantowej paczki falowej, która reprezentuje cząstkę, prędkość grupowa okazuje się związana ze średnią prędkością tej cząstki. Natomiast prędkość fazowa fali de Broglie’a może przyjmować wartości większe od prędkości światła, co mogłoby wydawać się sprzeczne z teorią względności, gdyby nie fakt, że to nie ona odpowiada za transport informacji. Takie przykłady pokazują, że właściwą wielkością do opisu dynamiki i przyczynowości jest właśnie prędkość grupowa, a nie fazowa.
Analiza dyspersji prowadzi także do pojęcia wyższych pochodnych relacji dyspersyjnej. O ile pierwsza pochodna mówi o prędkości grupowej, o tyle druga opisuje, jak ta prędkość zmienia się wraz z liczbą falową lub częstotliwością. W praktyce telekomunikacyjnej odpowiada to tak zwanej dyspersji chromatycznej, która jest odpowiedzialna za rozmywanie impulsów optycznych przesyłanych na duże odległości. Projektowanie nowoczesnych włókien światłowodowych i systemów kompensacji dyspersji wymaga szczegółowego zrozumienia zarówno prędkości grupowej, jak i jej zależności od widma sygnału.
Prędkość grupowa a transport energii i informacji
Jedną z najważniejszych ról prędkości grupowej jest opis transportu energii. W wielu sytuacjach fizycznych strumień energii związany z falą jest proporcjonalny do iloczynu gęstości energii i prędkości grupowej. Oznacza to, że tam, gdzie paczka falowa porusza się szybciej, energia jest przenoszona sprawniej na jednostkę czasu. To rozumowanie można zastosować zarówno w akustyce, gdzie fale dźwiękowe transportują energię mechanicznych drgań, jak i w optyce falowej, w której promień światła niesie energię elektromagnetyczną.
Prędkość grupowa jest także związana z tym, co potocznie nazywamy prędkością sygnału. Gdy wysyłamy impuls wzdłuż przewodu lub przez ośrodek, interesuje nas, jak szybko informacja o tym sygnale dotrze do odbiorcy. Chociaż poszczególne składowe falowe mogą mieć różne fazy i propagować się z różnymi prędkościami fazowymi, to kształt całego sygnału – jego maksimum, front, struktura modulacji – jest determinowany przez prędkość grupową i dyspersję.
Istotne jest jednak subtelne rozróżnienie między prędkością grupową a prędkością frontu fali. Front to granica między obszarem, gdzie amplituda jest dokładnie równa zero, a obszarem, w którym pojawia się sygnał. Z punktu widzenia teorii względności to właśnie prędkość frontu, a nie grupy, nie może przekroczyć prędkości światła w próżni. W niektórych silnie dyspersyjnych ośrodkach można skonstruować sytuacje, w których formalnie obliczona prędkość grupowa jest większa niż prędkość światła, a nawet przyjmuje wartości ujemne. Nie oznacza to jednak możliwości przesyłania informacji szybciej niż światło, gdyż front fali wciąż porusza się zgodnie z ograniczeniami relatywistycznymi.
Z punktu widzenia inżynierii komunikacyjnej, na przykład w systemach światłowodowych, prędkość grupowa stanowi kluczowy parametr określający opóźnienia sygnału. Projektując sieci transmisyjne, bierze się pod uwagę nie tylko samą wartość prędkości, ale przede wszystkim jej zależność od częstotliwości, która prowadzi do rozmywania impulsów. Wykorzystuje się tam specjalne profile refrakcyjne włókien, dzięki którym dyspersja może zostać zminimalizowana lub celowo ukształtowana, aby kompensować inne efekty. Bez precyzyjnej kontroli nad prędkością grupową trudno byłoby osiągnąć wysokie przepływności i małe błędy w transmisji danych.
Prędkość grupowa ma także znaczenie w geofizyce, gdzie analiza rozchodzenia się fal sejsmicznych pozwala badać strukturę wnętrza Ziemi. Różne typy fal sejsmicznych – podłużne, poprzeczne, powierzchniowe – mają własne relacje dyspersyjne, zależne od głębokości, gęstości i sprężystości skał. Porównanie obserwowanych czasów przybycia fal o różnych częstotliwościach umożliwia rekonstrukcję prędkości grupowych w różnych warstwach geologicznych. To z kolei dostarcza informacji o budowie skorupy, płaszcza i jądra, jak również o procesach tektonicznych i ryzyku sejsmicznym.
Dyspersja, zniekształcenia impulsów i zastosowania technologiczne
W ośrodkach dyspersyjnych prędkość grupowa zależy od częstotliwości, co prowadzi do zjawiska zwanego rozchodzeniem się paczki falowej. Jeśli impuls składa się z szerokiego widma, to poszczególne składowe poruszają się z różnymi prędkościami, a ich interferencja zmienia się w czasie. Efektem makroskopowym jest zniekształcenie kształtu impulsu: jego maksimum może przesunąć się, ogon wydłużyć, a amplituda obniżyć. W skrajnych przypadkach początkowo krótki impuls rozciąga się tak bardzo, że przestaje dawać się odróżnić od tła lub innych sygnałów.
W telekomunikacji światłowodowej problem dyspersji jest jednym z głównych ograniczeń długości odcinków między wzmacniakami lub regeneratorami. Włókno szklane wykazuje zależność współczynnika załamania od częstotliwości, co powoduje, że różne składowe spektralne impulsu docierają do odbiorcy w różnym czasie. By temu przeciwdziałać, stosuje się techniki kompensacji dyspersji, na przykład specjalne odcinki włókien o odwrotnym znaku dyspersji, siatki dyfrakcyjne, a także cyfrowe algorytmy equalizacji. Wszystkie takie rozwiązania bazują na precyzyjnym modelowaniu prędkości grupowej i jej zmienności.
Niektóre zaawansowane technologie optyczne, jak lasery z modulacją częstotliwości, wzmacniacze parametryczne czy nieliniowe kryształy do generacji nowych częstotliwości, wymagają ścisłego dopasowania prędkości fazowych i grupowych w różnych pasmach. Mówi się wtedy o dopasowaniu fazowym i dopasowaniu prędkości grupowej. Jeżeli prędkości grupowe fal biorących udział w procesie są zbyt różne, energie nie kumulują się efektywnie, a konwersja częstotliwości jest nieefektywna. Z kolei przy odpowiednim dopasowaniu można uzyskać bardzo wydajne procesy nieliniowe, takie jak generacja drugiej harmonicznej czy mieszanie fal.
W elektronice wysokich częstotliwości i w technice mikrofalowej analiza prędkości grupowej linii transmisyjnych jest kluczowa dla projektowania układów dopasowanych impedancyjnie i minimalizujących odbicia. Linia mikropaskowa, współosiowy przewód czy falowód prostokątny mają własne relacje dyspersyjne, wynikające z geometrii i dielektrycznych właściwości ośrodka. Prędkość grupowa w tych strukturach decyduje o czasie propagacji sygnału między układami, a także o tym, jak szerokopasmowe impulsy będą się rozmywać podczas przejścia przez skomplikowane topologie obwodów drukowanych.
Interesującym obszarem badań są materiały o inżynierowanych własnościach dyspersyjnych, tak zwane metamateriały. Dzięki okresowej strukturze na skalę mniejszą niż długość fali można uzyskać skuteczny współczynnik załamania o nietypowych wartościach, w tym ujemnych. Takie materiały mogą wykazywać anomalne zachowanie prędkości grupowej, prowadząc do zjawisk typu superluminalnej lub ujemnej prędkości grupowej w wąskich zakresach częstotliwości. Mimo że nie narusza to zasad przyczynowości, otwiera to drogę do konstrukcji kompaktowych urządzeń filtrujących, soczewek płaskich i zaawansowanych układów kontroli frontu falowego.
Innym ważnym zastosowaniem koncepcji prędkości grupowej są techniki obrazowania medycznego i przemysłowego oparte na falach ultradźwiękowych. Tkaniny biologiczne, jak i metale czy kompozyty, mogą mieć złożone własności dyspersyjne. Analizując, jak rozchodzą się paczki falowe w różnych zakresach częstotliwości, można wyciągać wnioski o strukturze wewnętrznej materiału, o obecności defektów, pęknięć czy zmian patologicznych. W tym kontekście znajomość prędkości grupowej i jej zależności od parametrów ośrodka staje się narzędziem diagnostycznym o dużej wartości praktycznej.
Prędkość grupowa w mechanice kwantowej i fizyce relatywistycznej
W mechanice kwantowej cząstki materialne, takie jak elektrony czy neutrony, opisuje się za pomocą funkcji falowej. W prostym przybliżeniu jednowymiarowa funkcja falowa może być traktowana jako paczka falowa zbudowana z fal de Broglie’a o różnych liczbach falowych. W takim ujęciu prędkość grupowa paczki odpowiada średniej prędkości cząstki, natomiast rozmywanie paczki w czasie związane jest z nieoznaczonością położenia i pędu. Destrukcja i rekonstrukcja przestrzennej lokalizacji cząstki widoczna jest w eksperymentach z dyfrakcją, interferencją czy tunelowaniem.
Relacja między energią, pędem a liczbą falową i częstością w mechanice kwantowej prowadzi do specyficznej relacji dyspersyjnej. Dla swobodnej cząstki nierelatywistycznej częstość jest proporcjonalna do kwadratu liczby falowej, co oznacza, że mamy do czynienia z silnie dyspersyjnym ośrodkiem. W takim przypadku prędkość grupowa zależy wprost od pędu, a paczka falowa szybko się rozmywa. Dla cząstki relatywistycznej relacja dyspersyjna zmienia się tak, że prędkość grupowa dąży do wartości prędkości światła w granicy dużych energii, odzwierciedlając fakt, że żaden obiekt materialny nie może jej przekroczyć.
Rozróżnienie między prędkością grupową a fazową nabiera szczególnego znaczenia przy analizie fal elektromagnetycznych w ośrodku i w próżni. W próżni fale świetlne mają liniową relację dyspersyjną, co prowadzi do zbieżności prędkości fazowej i grupowej. W ośrodkach dyspersyjnych, takich jak szkło, woda czy plazma, relacja ta jest już nieliniowa, a prędkości te różnią się. Niezależnie jednak od złożoności dyspersji, teoria względności wymaga, aby żadna wielkość fizyczna odpowiedzialna za przekazywanie informacji nie przekraczała prędkości światła w próżni. W rezultacie wszelkie pozornie superluminalne efekty prędkości grupowej są wynikiem subtelnej gry interferencyjnej i nie pozwalają na złamanie przyczynowości.
Analiza prędkości grupowej w kontekście relatywistycznym pojawia się również w badaniach nad propagacją fal w zakrzywionej czasoprzestrzeni, na przykład w otoczeniu czarnych dziur czy we wczesnym Wszechświecie. Fale grawitacyjne, które zostały bezpośrednio zarejestrowane przez detektory interferometryczne, mają relację dyspersyjną zbliżoną do tej, jaką mają fale świetlne w próżni. Weryfikując prędkość grupową fal grawitacyjnych, fizycy testują ogólną teorię względności oraz alternatywne modele grawitacji. Odchylenia od oczekiwanej wartości mogłyby sugerować istnienie masy grawitonu lub modyfikacje struktury czasoprzestrzeni na dużych skalach.
W teorii pól kwantowych i w fizyce ciała stałego, pojęcie prędkości grupowej rozszerza się na quasi-cząstki, takie jak fonony, magnony czy ekscytony. Te kolektywne wzbudzenia w sieciach krystalicznych opisuje się przy pomocy relacji dyspersyjnych zależnych od wektora falowego w przestrzeni odwrotnej. Prędkość grupowa tych wzbudzeń określa, jak szybko przenoszone są energia cieplna, impulsy magnetyczne czy ładunek w materiałach. Projektowanie funkcjonalnych materiałów termoelektrycznych, magnonicznych czy optoelektronicznych wymaga więc precyzyjnego modelowania ich spektrów dyspersyjnych i wynikających z nich prędkości grupowych.
Interpretacje, paradoksy i granice intuicji
Rozważając prędkość grupową, trudno uniknąć zderzenia z kilkoma pozornymi paradoksami. Pierwszy z nich dotyczy sytuacji, gdy prędkość grupowa jest większa od prędkości światła lub ujemna. W silnie dyspersyjnych strukturach, jak komory rezonansowe czy metamateriały, matematyczna definicja prędkości grupowej może prowadzić do takich wyników. Jednocześnie eksperymenty i analiza teoretyczna pokazują, że żaden fragment sygnału, który mógłby nieść użyteczną informację, nie pojawia się u odbiorcy przed wysłaniem sygnału przez nadawcę. Dzieje się tak dlatego, że kształt paczki w takich warunkach ulega znacznym zniekształceniom, a to, co interpretujemy jako przesunięcie maksimum, jest efektem interferencyjnego przetasowania amplitud.
Drugi paradoks związany jest z tym, że prędkość grupowa nie zawsze idealnie pokrywa się z prędkością energii. W niektórych ośrodkach z silnymi stratami, gdzie energia fali jest intensywnie absorbowana i reemitowana lokalnie, definicja oparta stricte na pochodnej relacji dyspersyjnej może przestać odzwierciedlać faktyczny transport energii. W takich przypadkach bardziej adekwatne jest analizowanie gęstości i strumienia energii, a prędkość grupową traktować z ostrożnością. To przypomnienie, że definicje matematyczne, choć potężne, mają swoje zakresy stosowalności.
Trzecim obszarem, w którym intuicja może zawieść, jest przenoszenie pojęcia prędkości grupowej na bardzo krótkie impulsy, porównywalne z okresem dominującej częstotliwości. W przypadku ultrakrótkich impulsów laserowych trwających zaledwie kilka cykli optycznych, klasyczna definicja paczki falowej jako powoli modulowanej fali nośnej staje się wątpliwa. Opis takiego impulsu wymaga uogólnionych koncepcji, jak prędkość fazy obwiedni czy definicji opartych na analizie falkowej. Pokazuje to, że pojęcia fazy i grupy są głęboko powiązane z przyjętym modelem matematycznym i zakresem stosowanych przybliżeń.
Mimo tych subtelności, prędkość grupowa pozostaje jednym z podstawowych narzędzi w analizie zjawisk falowych. Łączy ona intuicyjny obraz przesuwającej się paczki energii z precyzyjnym formalizmem relacji dyspersyjnej. Z jednej strony pozwala projektować efektywne systemy komunikacyjne, z drugiej – służy jako test konsekwencji fundamentalnych teorii fizyki, takich jak mechanika kwantowa i teoria względności. Refleksja nad ograniczeniami i paradoksami prędkości grupowej uczy też pokory wobec modelowania złożonych zjawisk w przyrodzie, w których nasze intuicje, wykształcone na bazie codziennych doświadczeń, często okazują się niewystarczające.
FAQ: Najczęściej zadawane pytania o prędkość grupową
Co to jest prędkość grupowa i czym różni się od fazowej?
Prędkość grupowa to prędkość, z jaką przemieszcza się obwiednia paczki falowej, czyli obszar skupienia energii i informacji. Wynika z pochodnej częstości po liczbie falowej. Prędkość fazowa opisuje natomiast ruch punktów o stałej fazie fali sinusoidalnej. W ośrodku niedyspersyjnym obie prędkości są równe, ale w ośrodkach dyspersyjnych mogą się znacznie różnić i prowadzić do zniekształceń impulsów.
Czy prędkość grupowa może być większa od prędkości światła?
W silnie dyspersyjnych lub rezonansowych ośrodkach obliczona z relacji dyspersyjnej prędkość grupowa może formalnie przekraczać prędkość światła, a nawet przyjmować wartości ujemne. Nie oznacza to jednak, że informacja lub energia są naprawdę przenoszone szybciej niż światło. Dokładniejsza analiza pokazuje, że front fali – odpowiedzialny za przyczynowość – wciąż porusza się nie szybciej niż światło w próżni.
Dlaczego prędkość grupowa jest ważna w światłowodach?
W światłowodach informacja jest kodowana w impulsach optycznych, które są paczkami falowymi. Ich prędkość grupowa decyduje o czasie dotarcia sygnału od nadajnika do odbiornika. Ponieważ prędkość grupowa zależy od częstotliwości, dyspersja powoduje rozmywanie impulsów i może ograniczać przepustowość łącza. Projektanci sieci światłowodowych modelują i kontrolują prędkość grupową, aby minimalizować zniekształcenia i zwiększać szybkość transmisji danych.
Jak prędkość grupowa wiąże się z mechaniką kwantową?
W mechanice kwantowej cząstkę opisuje się jako paczkę falową złożoną z fal de Broglie’a o różnych liczbach falowych. Prędkość grupowa tej paczki odpowiada średniej prędkości cząstki, natomiast rozmywanie paczki w czasie odzwierciedla wzrost nieoznaczoności położenia. Relacja dyspersyjna wyprowadzona z równania Schrödingera określa, jak ta prędkość zależy od energii i pędu, a tym samym jakie są możliwe trajektorie i rozmycia w doświadczeniach kwantowych.
Czy prędkość grupowa zawsze opisuje transport energii?
W wielu prostych, słabo absorbujących ośrodkach prędkość grupowa jest dobrym przybliżeniem prędkości przepływu energii. W silnie stratnych lub silnie nieliniowych mediach ta zgodność może jednak zanikać. Wtedy lepiej analizować bezpośrednio gęstość i strumień energii. Prędkość grupowa nadal pozostaje użytecznym narzędziem matematycznym, ale jej interpretacja jako jednoznacznej prędkości transportu energii musi być traktowana ostrożnie i zależy od konkretnego układu.