Widmo sygnału jest jednym z kluczowych pojęć współczesnej nauki i techniki, łączącym teorię matematyczną z bardzo praktycznymi zastosowaniami – od telekomunikacji, przez medycynę, aż po analizę muzyki. Zrozumienie, czym jest widmo sygnału, pozwala zobaczyć w czasie to, czego nie widać gołym okiem: ukrytą strukturę częstotliwościową drgań, fal i procesów losowych. To właśnie dzięki analizie widmowej możliwe jest projektowanie efektywnych systemów komunikacyjnych, dokładnych przyrządów pomiarowych czy zaawansowanych algorytmów przetwarzania danych.
Intuicyjne i formalne rozumienie widma sygnału
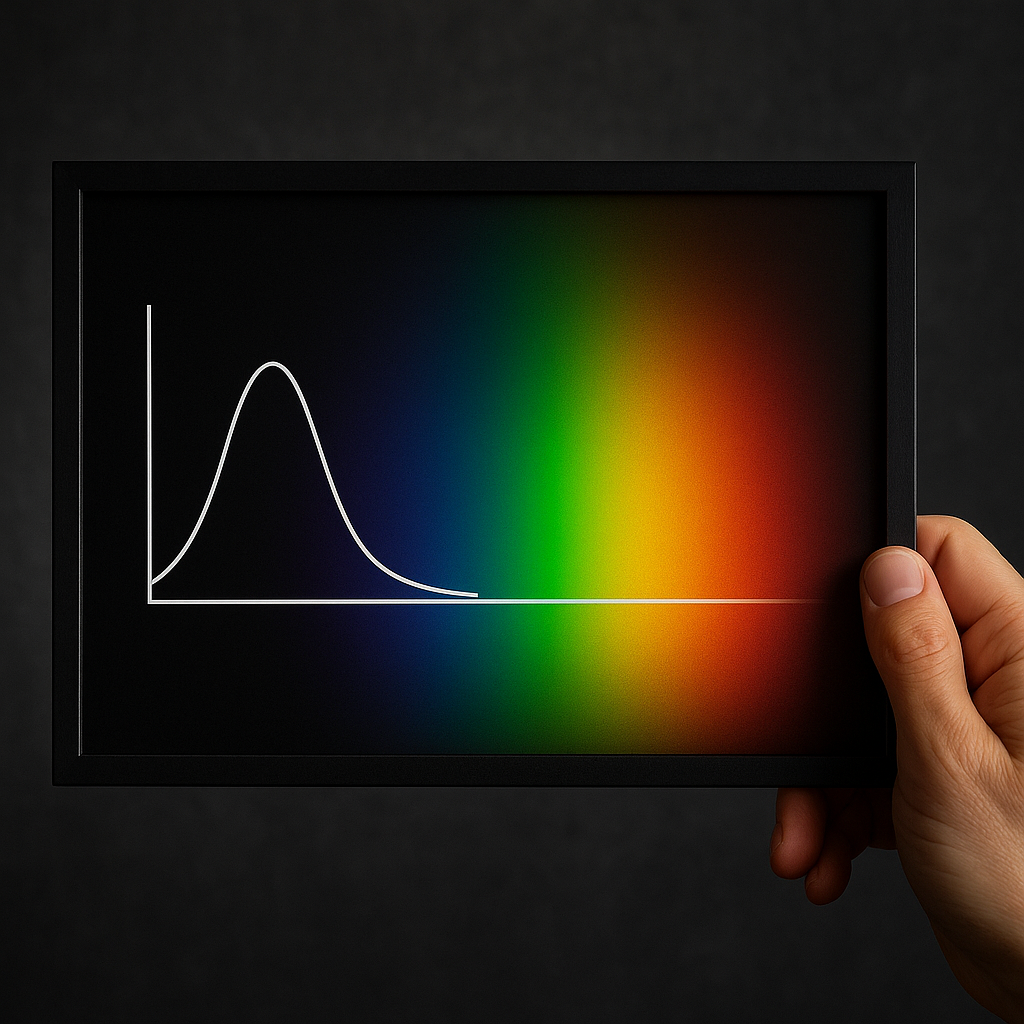
Najprostsza intuicja związana z widmem sygnału odwołuje się do muzyki. Każdy dźwięk, który słyszymy, może być opisany jako mieszanina tonów prostych – sinusoid o określonych częstotliwościach. W przypadku instrumentu muzycznego dźwięk ma tak zwany ton podstawowy oraz wyższe harmoniczne, czyli składowe o częstotliwościach będących wielokrotnościami tonu podstawowego. Jeżeli narysujemy, jakie częstotliwości są obecne w dźwięku i jak silne jest ich natężenie, otrzymamy właśnie jego widmo.
Widmo sygnału to zatem opis, jak rozkłada się energia lub moc sygnału w dziedzinie częstotliwości. Dla sygnału zależnego od czasu mówimy o transformacji z dziedziny czasu do dziedziny częstotliwości. W sensie matematycznym fundamentem takiej zamiany jest najczęściej transformata Fouriera, która pozwala rozłożyć niemal dowolny sygnał na nieskończony (lub skończony, w wersji dyskretnej) zbiór fal sinusoidalnych. Każda z tych fal ma własną częstotliwość, amplitudę i fazę, a wszystkie razem – po zsumowaniu – odtwarzają pierwotny przebieg czasowy.
Formalnie widmo ciągłego sygnału czasowego x(t) można zdefiniować jako funkcję X(f), będącą transformatą Fouriera sygnału. Funkcja X(f) opisuje udział poszczególnych częstotliwości f w sygnale x(t). Zależnie od kontekstu interesować może nas widmo amplitudowe (jakie są amplitudy składowych), widmo fazowe (jak wyglądają przesunięcia fazowe), a często widmo mocy, powiązane bezpośrednio z tym, jak energia sygnału rozkłada się w zakresie częstotliwości. W praktyce inżynierskiej często analizuje się wykres modułu X(f), ignorując fazę, choć w wielu zastosowaniach faza ma ogromne znaczenie, na przykład w rekonstrukcji sygnału, w stereofonii czy w obrazowaniu medycznym.
Ważne jest też rozróżnienie pomiędzy sygnałami deterministycznymi a losowymi. W pierwszym przypadku możemy mówić o transformatcie Fouriera konkretnego przebiegu, a w drugim – o gęstości widmowej mocy, opisującej statystyczne własności procesu losowego. Takie podejście jest niezbędne przy analizie szumów, drgań losowych czy sygnałów biologicznych, które z natury są zmienne i niepowtarzalne w czasie.
Transformata Fouriera i podstawowe typy widm
Kluczowym narzędziem w analizie widma sygnału jest transformata Fouriera. W wersji ciągłej przekształcenie to łączy sygnał w dziedzinie czasu z jego reprezentacją w dziedzinie częstotliwości. Intuicyjnie można myśleć o transformatcie jako o „przesiewaniu” sygnału przez zestaw sinusoid o różnych częstotliwościach. Dla każdej częstotliwości badamy, jak silnie jest ona obecna w sygnale, czego wynikiem jest funkcja X(f).
W praktyce jednak bardzo rzadko mamy do czynienia z sygnałami obserwowanymi ciągle. Większość współczesnych systemów cyfrowych pracuje na próbkach: komputer czy przetwornik A/C pobiera wartości sygnału w kolejnych chwilach czasu, co określa się mianem próbkowania. W takim przypadku podstawową rolę odgrywa dyskretna transformata Fouriera (DTF), a do jej szybkiego obliczania służy algorytm FFT, będący obecnie jednym z najważniejszych algorytmów numerycznych w inżynierii i naukach ścisłych.
Wyróżnić można kilka podstawowych rodzajów widm:
- Widmo amplitudowe – pokazuje amplitudy składowych sinusoidalnych w funkcji częstotliwości. Jest najczęściej rysowane na wykresach i używane do wizualnej oceny zawartości częstotliwościowej sygnału, np. w analizie dźwięku czy drgań mechanicznych.
- Widmo fazowe – prezentuje fazy poszczególnych składowych. Informacja fazowa jest krytyczna wszędzie tam, gdzie znaczenie ma dokładny kształt fali w czasie, a nie tylko jej „skład częstotliwościowy”. Brak fazy oznacza możliwość zachowania amplitud, ale utraty oryginalnej postaci sygnału.
- Widmo mocy – opisuje, jak moc sygnału jest rozłożona w funkcji częstotliwości. Jest szczególnie istotne w systemach telekomunikacyjnych, radiowych i radarowych, gdzie liczy się efektywne wykorzystanie zasobów energetycznych i spektralnych.
- Gęstość widmowa mocy – używana dla procesów losowych. Dla sygnałów takich jak szumy elektroniczne, fluktuacje w układach biologicznych czy zmienność klimatu, pojedyncza realizacja nie wystarcza; potrzebny jest opis probabilistyczny, który mówi, jak statystycznie rozkłada się moc w paśmie częstotliwości.
W praktyce obliczeniowej istotne jest także rozdzielenie widma na część rzeczywistą i urojoną, o czym rzadziej mówi się w zastosowaniach czysto inżynierskich. Jednak w analizie systemów liniowych, w teorii sterowania czy w mechanice kwantowej pełna, zespolona natura widma ma zasadnicze znaczenie. Moduł liczby zespolonej odpowiada za amplitudę, a argument za fazę. Dzięki temu widmo staje się nośnikiem kompletu informacji o sygnale, przy założeniu, że przekształcenie jest odwracalne.
Typowym problemem praktycznym jest aliasing, czyli zjawisko nakładania się widmowe wynikające z niedostatecznego próbkowania. Jeżeli częstotliwość próbkowania jest zbyt niska w stosunku do najwyższej składowej sygnału, widmo sygnału po próbkowaniu nakłada się samo na siebie, a w rezultacie informacje o wysokich częstotliwościach są błędnie odwzorowane jako niższe. Aby uniknąć aliasingu, stosuje się filtrację antyaliasingową i przestrzega się twierdzenia Nyquista-Shannona, które określa minimalną częstotliwość próbkowania jako co najmniej dwukrotnie wyższą od najwyższej istotnej częstotliwości w sygnale.
Widmo sygnału w praktyce inżynierskiej i naukowej
Widmo sygnału jest narzędziem uniwersalnym, dlatego pojawia się w ogromnej liczbie dziedzin. W telekomunikacji wykorzystywane jest do projektowania systemów transmisji, modulacji i multipleksacji. Dzięki analizie widmowej można określić, czy dany sygnał mieści się w przydzielonym paśmie częstotliwości, czy nie powoduje niepożądanych zakłóceń w sąsiednich kanałach oraz jak bardzo jest podatny na szumy. Projektując systemy bezprzewodowe, badacze dążą do jak najefektywniejszego upakowania informacji w ograniczonym paśmie. Tu widmo sygnału jest kluczowym kryterium optymalizacji.
W akustyce i przetwarzaniu dźwięku widma używa się do analizy właściwości instrumentów muzycznych, projektowania filtrów audio, kompresji danych dźwiękowych oraz syntezy mowy. W przypadku syntezy mowy algorytmy korzystają z wiedzy o tym, jak człowiek odbiera różne częstotliwości, a także jak energia mowy rozkłada się w widmie w zależności od artykułowanych głosek. Dzięki temu możliwe jest realistyczne generowanie dźwięku na podstawie abstrakcyjnych reprezentacji parametrów widmowych.
W medycynie widmo sygnału odgrywa istotną rolę w analizie sygnałów biologicznych, takich jak EEG (elektroencefalogram), EKG (elektrokardiogram) czy EMG (elektromiogram). Na przykład EEG bada się często w dziedzinie częstotliwości, wyodrębniając charakterystyczne pasma fal mózgowych: delta, theta, alfa, beta i gamma. Zmiany w widmie mogą wskazywać na różne stany fizjologiczne, zaburzenia snu, padaczkę czy reakcje na bodźce. Podobnie w kardiologii analiza widmowa pozwala wykrywać zaburzenia rytmu czy wskazywać na zmiany w autonomicznym układzie nerwowym.
Innym obszarem jest mechanika i diagnostyka maszyn. Sygnały drgań zbierane z czujników przyspieszeń lub przemieszczeń poddaje się analizie widmowej, aby wykryć uszkodzenia łożysk, niewyważenie wirników, luzy czy pęknięcia elementów konstrukcyjnych. Charakterystyczne częstotliwości pojawiające się w widmie mogą wskazywać, który element maszyny jest uszkodzony, a ich amplituda – na stopień zużycia. Takie podejście, zwane diagnostyką wibroakustyczną, stanowi podstawę nowoczesnych systemów monitoringu stanu technicznego.
Widmo sygnału wykorzystywane jest również w naukach o Ziemi i środowisku. Analizuje się w ten sposób wahania klimatu, zmiany poziomu morza, drgania sejsmiczne czy sygnały pochodzące z atmosfery. Na przykład widma czasowych zmian temperatury pozwalają identyfikować okresowe komponenty związane z cyklem dobowym, rocznym i wieloletnim. W sejsmologii różne typy fal sejsmicznych mają odmienne charakterystyki widmowe, co pozwala na ich rozróżnienie oraz wnioskowanie o strukturze wnętrza Ziemi.
Wreszcie, w fizyce i astronomii pojęcie widma sygnału rozszerza się na widmo elektromagnetyczne i widma emisyjne oraz absorpcyjne atomów i cząsteczek. Choć mowa tu o widmach częstotliwościowych w sensie fal elekromagnetycznych, matematyczne podstawy są podobne. Analiza widmowa światła gwiazd czy galaktyk pozwala określać skład chemiczny, temperaturę, prędkości radialne obiektów oraz wiele innych parametrów. Z kolei spektroskopia w laboratorium umożliwia badanie struktury cząsteczek, reakcji chemicznych i oddziaływań międzycząsteczkowych, opierając się na szczegółowej analizie widma absorpcji lub emisji promieniowania.
Coraz większą rolę odgrywa także analiza widmowa w przetwarzaniu obrazów i w wizji komputerowej. Choć obrazy są funkcjami dwóch (lub więcej) zmiennych przestrzennych, a nie czasu, można stosować dwuwymiarową transformatę Fouriera. Widmo obrazu opisuje rozkład przestrzennych częstotliwości, co jest przydatne przy filtracji, kompresji i rekonstrukcji. Filtry dolno- i górnoprzepustowe w dziedzinie częstotliwościowej pozwalają wygładzać obrazy lub podkreślać krawędzie i drobne detale. W ten sposób idea widma sygnału przenika do bardzo odmiennych od siebie dziedzin.
Ograniczenia, pułapki i rozwinięcia analizy widmowej
Mimo ogromnej użyteczności analiza widmowa ma swoje ograniczenia. Jednym z najczęściej dyskutowanych jest kompromis między rozdzielczością czasową a częstotliwościową. Klasyczna transformata Fouriera zakłada analizę całego sygnału na raz, co jest idealne dla sygnałów stacjonarnych, których własności nie zmieniają się w czasie. W przypadku sygnałów niestacjonarnych, takich jak mowa, muzyka, sygnały biologiczne czy zjawiska atmosferyczne, interesuje nas, jak widmo zmienia się w czasie. Aby rozwiązać ten problem, stosuje się krótkoczasową transformację Fouriera (STFT), w której sygnał dzielony jest na krótkie okna czasowe. Każde okno podlega osobnej transformacji, a wynik tworzy reprezentację czasowo-częstotliwościową.
Jednak długość okna tworzy fundamentalny kompromis: krótsze okno zapewnia dobrą rozdzielczość czasową, ale gorszą częstotliwościową; dłuższe okno – odwrotnie. Ten kompromis ma naturę związaną z zasadą nieoznaczoności, znaną także z mechaniki kwantowej. Oznacza on, że nie da się arbitralnie precyzyjnie wyznaczyć zarówno momentu wystąpienia zjawiska, jak i jego częstotliwości. To ograniczenie ma charakter ogólny i wynika z matematycznych właściwości transformacji Fouriera.
Aby lepiej radzić sobie z sygnałami niestacjonarnymi o złożonej strukturze, opracowano alternatywne metody, takie jak analiza falkowa. Falelet, czyli funkcje o lokalnym zasięgu w czasie i częstotliwości, pozwalają adaptacyjnie dopasowywać rozdzielczość: dla wysokich częstotliwości stosuje się krótsze okna, a dla niskich – dłuższe. Taki sposób widzenia widma sygnału jest szczególnie pożyteczny w analizie sygnałów z nagłymi, krótkotrwałymi zdarzeniami, jak wyładowania elektryczne, trzaski czy fale uderzeniowe. Analiza falkowa bywa także używana do kompresji danych i odszumiania, ponieważ dobrze wydziela struktury lokalne.
W praktyce obliczeniowej dochodzą kwestie takie jak wybór okna analitycznego. Aby ograniczyć efekty obcięcia sygnału w skończonym przedziale czasu, stosuje się różne funkcje okna: prostokątne, Hanninga, Hamminga, Blackmana i inne. Wybór okna wpływa na kształt głównej wiązki i poziom listków bocznych w widmie, a tym samym na zdolność do rozdzielania bliskich częstotliwości i tłumienia „przecieków widmowych”. Jest to klasyczny przykład zjawiska, w którym matematykę i inżynierię łączy kompromis pomiędzy rozdzielczością a dokładnością.
Dodatkowym zagadnieniem są szumy i zakłócenia. W idealnym świecie widmo sygnału reprezentowałoby wyłącznie użyteczną informację. W rzeczywistości praktycznie każdy pomiar obarczony jest szumem, którego widmo często bywa szerokopasmowe. Sztuka polega na takim kształtowaniu systemu pomiarowego, filtrów i algorytmów przetwarzania, aby maksymalnie zwiększyć stosunek sygnału do szumu. W tym celu projektuje się filtry pasmowo-przepustowe, dopasowane, adaptacyjne czy cyfrowe filtry o zadanej charakterystyce. Analiza widmowa jest tutaj narzędziem zarówno diagnostycznym, jak i projektowym, pozwalając ocenić, czy w danym paśmie częstotliwości sygnał jest wystarczająco silny w stosunku do tła szumowego.
Widmo sygnału znalazło też swoje miejsce w uczeniu maszynowym i analizie danych. Reprezentacje czasowo-częstotliwościowe sygnałów akustycznych, takie jak spektrogramy, są wykorzystywane jako dane wejściowe do sieci neuronowych klasyfikujących mowę, dźwięki środowiskowe czy muzykę. W medycynie neurofizjologicznej uczenie maszynowe na widmach sygnałów EEG pozwala identyfikować stany poznawcze, wykrywać napady padaczkowe czy wspomagać interfejsy mózg–komputer. Tutaj widmo staje się formą cechy, kodującą istotne właściwości sygnału w postaci, z którą algorytmy potrafią skutecznie pracować.
Wreszcie, rozwijają się nowe koncepcje widma sygnału, związane z nieliniową analizą i teorią chaosu. W przypadku systemów silnie nieliniowych klasyczna transformata Fouriera bywa niewystarczająca; pojawiają się zjawiska takie jak generacja nowych częstotliwości, modulacje złożone czy wielostabilność. Stosuje się wtedy metody oparte na transformacjach czasowo-częstotliwościowych, rozkładach empirycznych czy analizie modalnej, które pozwalają wydzielać dominujące tryby drgań. W ten sposób pojęcie widma sygnału wciąż ewoluuje, obejmując coraz szersze klasy zjawisk fizycznych, biologicznych i technicznych.
FAQ – najczęstsze pytania o widmo sygnału
Czym praktycznie jest widmo sygnału i jak je „zobaczyć”?
Widmo sygnału to opis, jak energia lub moc sygnału rozkłada się pomiędzy różne częstotliwości. Aby je zobaczyć, rejestruje się sygnał w czasie, a następnie oblicza jego transformatę Fouriera lub FFT. Otrzymujemy wykres, na którym oś pozioma to częstotliwość, a pionowa – amplituda lub moc. Analizując taki wykres, można łatwo wykryć dominujące składowe, obecność zakłóceń czy szumów w określonych pasmach.
Jakie są najważniejsze różnice między widmem sygnału ciągłego a dyskretnego?
Widmo sygnału ciągłego jest z definicji ciągłą funkcją częstotliwości; opisuje sygnał, który istnieje w każdej chwili czasu. W przypadku sygnału dyskretnego mamy do czynienia z próbkami pobieranymi z określoną częstotliwością. Jego widmo jest okresowe i ograniczone pasmem sięgającym do połowy częstotliwości próbkowania. Niedostateczne próbkowanie prowadzi do aliasingu, czyli nakładania się składowych widmowych, co zniekształca informację o wysokich częstotliwościach.
Dlaczego w analizie widmowej stosuje się różne okna i czym one są?
Okna w analizie widmowej to funkcje, którymi mnoży się fragment sygnału przed obliczeniem transformaty Fouriera. Ich zadaniem jest zmniejszenie efektów obcinania sygnału w skończonym przedziale czasu, co redukuje tzw. przecieki widmowe. Różne okna, jak Hanninga czy Hamminga, mają odmienny kształt i zapewniają różny kompromis między szerokością głównej wiązki a poziomem listków bocznych. Wybór odpowiedniego okna wpływa na zdolność rozdzielania bliskich częstotliwości i tłumienie artefaktów.
W jakich zastosowaniach faza widma ma kluczowe znaczenie?
Faza jest krytyczna wtedy, gdy liczy się dokładny kształt sygnału w czasie lub przestrzeni. Przykładowo, w rekonstrukcji dźwięku z widma utrata informacji fazowej prowadzi do istotnego zniekształcenia brzmienia. W obrazowaniu medycznym i radarowym faza odpowiada za precyzję pozycjonowania obiektów. W interferometrii astronomicznej niespójność fazowa między teleskopami ogranicza rozdzielczość obrazów. Ignorowanie fazy bywa wygodne obliczeniowo, ale w wielu zadaniach obniża jakość rekonstrukcji.
Czy widmo sygnału można stosować do analizy zjawisk niestacjonarnych, jak mowa czy EEG?
Tak, ale wymaga to rozszerzenia klasycznej analizy Fouriera. Stosuje się krótkoczasową transformatę Fouriera (STFT) lub analizę falkową, które dostarczają reprezentacji czasowo-częstotliwościowej. Sygnał dzieli się na krótkie fragmenty, dla których oblicza się lokalne widma. Pozwala to śledzić, jak zmienia się zawartość częstotliwościowa w czasie. Jest to podstawowe narzędzie w fonetyce, rozpoznawaniu mowy, analizie EEG czy badaniu krótkotrwałych zjawisk fizjologicznych.